具有高散熱性能的陶瓷基板用于大功率電子設備，本文主要研究活性材料釬焊（AMB）陶瓷基板制造過程中產生的翹曲變形和殘余應力。為了基板設計提供重要的參數，并確保良好的可靠性。在有限元用于分析陶瓷、金屬和焊料厚度、陶瓷基板尺寸和壓力對殘余應力分布和翹曲變形的影響。

比較了熱彈性和熱彈塑性有限元的計算結果，在焊接過程中的塑性變形過程極大地影響計算結果的準確性，發現最大軸向應力集中在陶瓷側，軸向殘余應力是引起陶瓷基體開裂的主要因素。陶瓷、金屬和焊料的厚度以及基板尺寸對殘余應力有顯著影響和翹曲變形，在這兩者都可以通過施加外部壓力來減少。

與傳統的塑料基印刷電路板相比，陶瓷基板具有更好的導熱性。陶瓷基板與較厚的金屬層相結合，可用于在極端環境下運行的大功率電子設備。常用的陶瓷材料有AIN、AI2O3和Si3N4。具有170W/mk的高導熱率的AIN基板，提供了一個很好的替代傳統的24W/mk的氧化鋁（AI2O3）基板，以實現更好的散熱。然而，AlN襯底(α= 4.3 ppm/℃)仍然存在與銅(α= 16.3 ppm/℃)不匹配的高熱膨脹系數(CTE)。活性材料釬焊（AMB）陶瓷基板是直接鍵合銅（DBC）的進一步發展，它基于陶瓷和活性元素在高溫下的反應。因此，AMB陶瓷基板具有更高的結合力和可靠性。

冷卻過程中陶瓷金屬界面處會產生殘余應力，由于CTE不匹配殘余應力值受以下因素影響很多因素。殘余應力對陶瓷金屬有很大影響界面性能。較大的變形導致蝕刻減少精度，而較高的殘余應力會降低抗疲勞性和使用壽命。因此，在控制基板變形和減少殘余應力對提高精度和使用性能具有重要意義。

確定薄膜殘余應力的最常用方法是基于在基板方面的基板彎曲變形曲率半徑。薄膜中的殘余應力可以使用計算斯托尼方程：

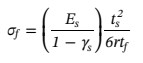
其中，Es和γs分別是楊氏模量和泊松比基材，ts和tf分別代表基板和薄膜的厚度。該公式的準確條件之一是薄膜比基材薄得多。然而，在本文中金屬層厚度與陶瓷基板的厚度比較接近，在冷卻過程中金屬會發生塑性變形。當基板的厚度接近薄膜時，或在殘余應力作用下的結構發生較大變形時，都會影響殘余應力結果的準確性。在這里殘余應力是使用有限元法(FEM)計算的，以確保結果的準確性。

由于材料的厚度是可變的，因此不應使用曲率半徑來測量界面處的應力。熱的殘余應力可以用方程式表示，這不需要考慮材料厚度：

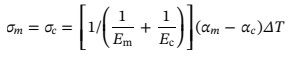
其中，Em是金屬的彈性模量，Ec是金屬的彈性模量陶瓷，αm是金屬的熱膨脹系數，αc是陶瓷的熱膨脹系數，ΔT是從高到低的冷卻間隔。該公式只計算了彈性范圍內的接頭熱殘余應力，沒有考慮材料性能隨溫度的變化，因此計算結果存在較大偏差。

有限元法已被廣泛用于預測殘差釬焊連接處的應力，然而關于AMB陶瓷基板殘余應力和變形的研究尚未有結果，在采用有限元分析方法分析了影響不銹鋼板翅結構殘余應力的因素。結果表明，材料失配。釬焊間隙、壓力載荷、翅片間距、厚度和高度，以及板厚顯著影響殘差應力分布。研究表明釬焊的Si3N4/42CrMo接頭的熱應力分布活性填料，結果表明，在峰值拉伸軸向殘余應力總是出現在Si3N4陶瓷中。現已經有很多文章研究下DBC陶瓷基板的應力變化循環加熱條件。對直接鍍銅(DPC)氮化鋁(AlN)進行了有限元研究基質，它也是從經過驗證的有限元模擬中發現的銅膜楔角、長度和厚度顯著影響熱循環加載過程中AlN的最大第一主應力。

在本文中，陶瓷金屬和焊料厚度的影響。隨著陶瓷基板尺寸和殘余應力壓力和釬焊過程中產生的翹曲變形分析如下：有限元分析的下，該研究有助于控制生產過程中的殘余應力和變形。目前，在殘余應力和變形的計算通常通過數值模擬來實現。在仿真過程中，陶瓷基板可以不受機械約束地自由翹曲。本文研究旨在了解陶瓷基板殘余熱應力的形成機理，掌握其變形規律及主要影響因素。

一、有限元模型

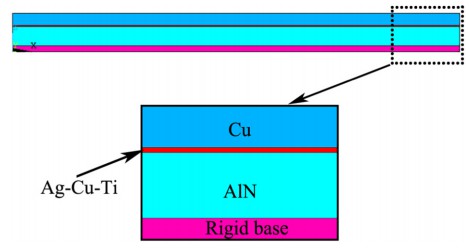
基于熱彈塑性應力應變行為并考慮材料特性隨溫度的變化，ANSYS用于分析AMB陶瓷基板的殘余應力和變形。該模型為單面陶瓷基板，如圖1所示，以10 °C/min的速度將樣品從 800 °C 冷卻至室溫冷卻速度。不考慮反應層分析，因為它太薄，相變的影響是忽略。假設冷卻過程中的樣品溫度是均勻的，具有完美的界面附著力。此外，計算中沒有考慮界面強化的影響。采用 von-Mises 屈服準則，等效應力為：

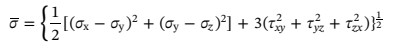
模型采用3D彈塑性有限元分析方法。使用8節點對模型進行網格劃分，在模擬中過程中，對模型施加的約束如圖2所示。將樣品和剛性底座設置為接觸對，使樣品可以自由彎曲。采用1/4對稱模型來簡化有限元計算。

二、殘余應力和翹曲結果

1、熱彈性和熱塑性有限元的比較

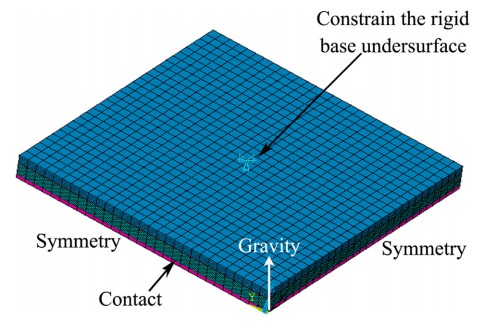
本文對熱彈性有限元的計算結果將熱彈塑性有限元法與熱彈塑性有限元法進行比較，熱彈塑性有限元法計算的結果更接近實際測量結果。在這個模型中，陶瓷的厚度是0.635毫米，銅金屬層的厚度為0.3毫米，厚度為Ag-Cu-Ti 焊料層為 50 μm。樣品的變形為用數顯高度計測量，如圖3所示。如果塑料不考慮焊接過程的變形，可靠性計算量會大大減少。但是，計算結果熱彈塑性有限元模型更適合實際

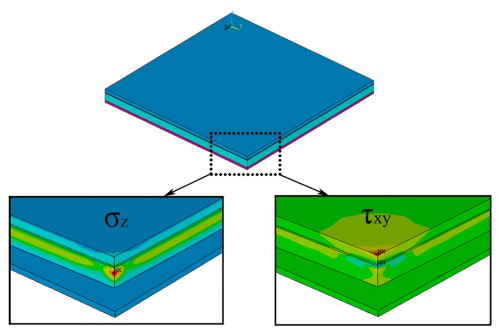
本文對熱彈性有限元的計算結果將熱彈塑性有限元法與熱彈塑性有限元法進行比較，熱彈塑性有限元法計算的結果更接近實際測量結果。在這個模型中，陶瓷的厚度是0.635毫米，銅金屬層的厚度為0.3毫米，厚度為Ag-Cu-Ti焊料層為50 μm。樣品的變形為用數顯高度計測量，如圖3所示。如果塑料不考慮焊接過程的變形，可靠性計算量會大大減少。但是計算結果熱彈塑性有限元模型更適合實際情況和計算是可靠的。根據調查結果如圖4拐角區域試樣的剪應力計算和軸向殘余應力圖可知，軸向拉伸應力是陶瓷基板失效的主要因素。

 2、陶瓷厚度對翹曲和殘余應力的影響

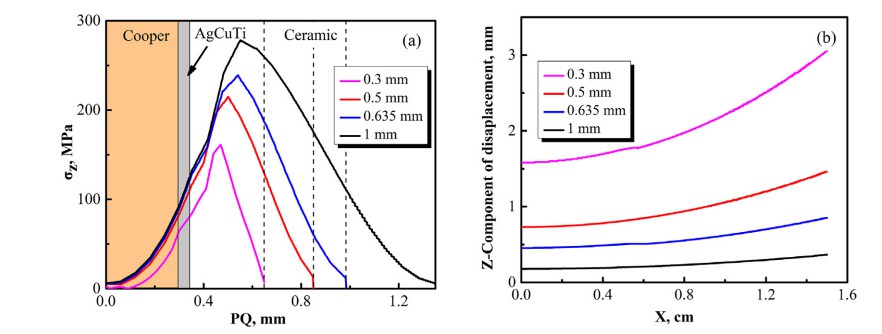
不僅影響軸向殘余應力和翹曲變形，由材料的熱膨脹系數和尺寸決定的基板。不同陶瓷厚度的有限元模型模擬揭示了陶瓷厚度對翹曲變形和殘余應力的有影響。銅膜厚度為0.3mm，Ag-Cu-Ti填充金屬層為50μm，面積為陶瓷基板保持不變。軸向殘余應力和陶瓷基板的翹曲變形圖，厚度為0.635mm如圖5a和圖5b所示。從軸向殘差應力圖，最大軸向應力集中在陶瓷上邊。可不同陶瓷沿PQ路徑的σz分布厚度如圖6a所示。可以看出來，陶瓷厚度變化對最大σz有很大影響。

當陶瓷厚度增加，殘余應力分布保持不變基本不變，但峰值應力增加。很明顯陶瓷厚度越大，軸向應力越大。此外，可以看出軸向應力是拉伸的，如圖6b所示陶瓷厚度與z分量的關系。沿MN路徑的位移，需要注意X定義為長度從M到N，表明隨著陶瓷厚度的增加，整體翹曲逐漸減小。從圖6(a)和圖6(b)可以看出，對應陶瓷厚度的最大軸向殘余應力0.3mm、0.5mm、0.635mm和1mm分別為161 MPa、215 MPa、239 MPa和278兆帕。分別對應陶瓷厚度0.3 mm、0.5 mm、0.635 mm和1 mm的最大軸向位移分別為3.165毫米、1.47毫米、0.922毫米和0.376毫米。什么時候陶瓷厚度為0.3 mm，變形最大，相應陶瓷基板的軸向應力最小。

3、銅層厚度對翹曲和殘余應力的影響

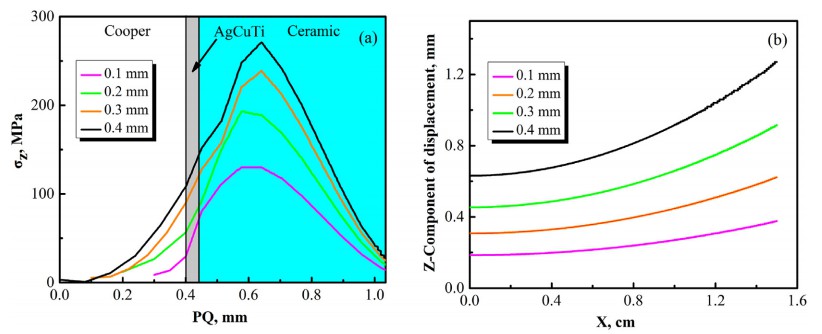
陶瓷基板的銅層厚度是一個重要參數，這對翹曲變形和軸向殘余應力很重要發展。為了研究銅層厚度效應，四種FEM型號，帶0.1 mm、0.2 mm、0.3 mm 和 0.4 mm銅厚度被開發出來。軸向殘余應力分布PQ 路徑和沿 MN 路徑位移的Z分量不同銅層厚度的陶瓷基板如圖所示圖7(a)和圖7(b)。表明軸向殘余應力增加銅厚。銅層厚度0.1 mm、0.2 mm、0.3 mm和0.3 mm 對應的最大軸向殘余應力0.4 mm分別為 140 MPa、200 MPa、239 MPa和271 MPa。這銅層厚度0.1mm、0.2mm、0.3mm、0.4mm對應的最大軸向位移為0.207mm、0.626mm，

分別為 0.922毫米和1.277毫米。對于0.1毫米厚的銅層，陶瓷基板的變形梯度很小，從而減少殘余應力。隨著金屬厚度的增加，沿PQ路徑的殘余軸向應力的總體趨勢沒有改變顯著，但應力峰值增加。

4、焊料厚度對翹曲和殘余應力的影響

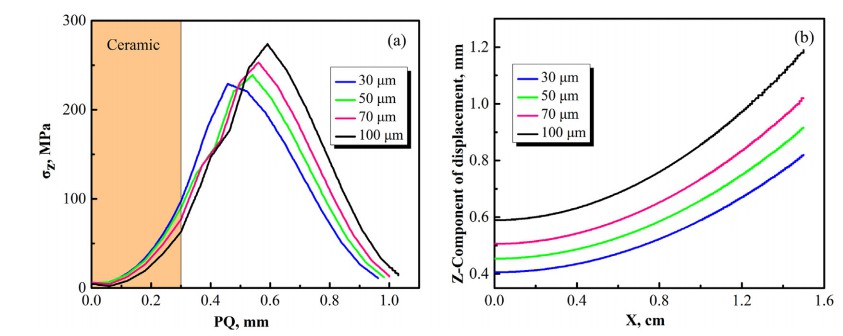
在本節中，設計了四個模型來研究焊料層厚度對翹曲變形和殘余應力的影響AMB陶瓷基板：30 μm、50 μm、70 μm和100 μm。焊料層厚度對沿PQ路徑和Z分量的軸向應力的影響沿MN路徑的位移如圖8所示。軸向應力隨焊料層厚度增加。最大軸向殘差對應于30 μm、50 μm、70 μm 焊料厚度的應力100 μm分別為229 MPa、239 MPa、253 MPa和278 MPa。焊料厚度對應的最大軸向位移30 μm、50 μm、70 μm 和 100 μm 分別為 0.826 mm、0.922 mm、1.026 mm和 1.193 毫米分別。

5、基板尺寸對翹曲和殘余應力的影響

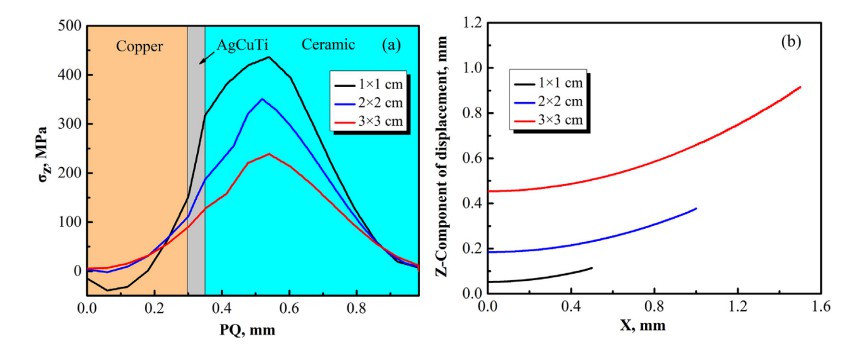
通過考慮基板的尺寸進行了類似的分析，如圖9所示。當基板的尺寸從1 × 1 cm到2 × 2 cm和 3 × 3 cm，翹曲變形增加。然而，軸向殘余應力隨著增加而減小基板尺寸。對應的最大軸向殘余應力為1 × 1 cm、2 × 2 cm和3 × 3 cm尺寸分別為 436 MPa、350 MPa和分別為 239 兆帕。對應的最大軸向位移到1 × 1 厘米、 2 × 2厘米和3 × 3厘米大小是0.114毫米、 0.377 毫米和分別為0.922毫米。隨著樣本量的減小，趨勢殘余應力分布發生了變化。對于1 cm × 1 c的樣品，沿PQ路徑的軸向殘余應力分布不完全是拉伸的，它從拉伸變為壓縮從界面。

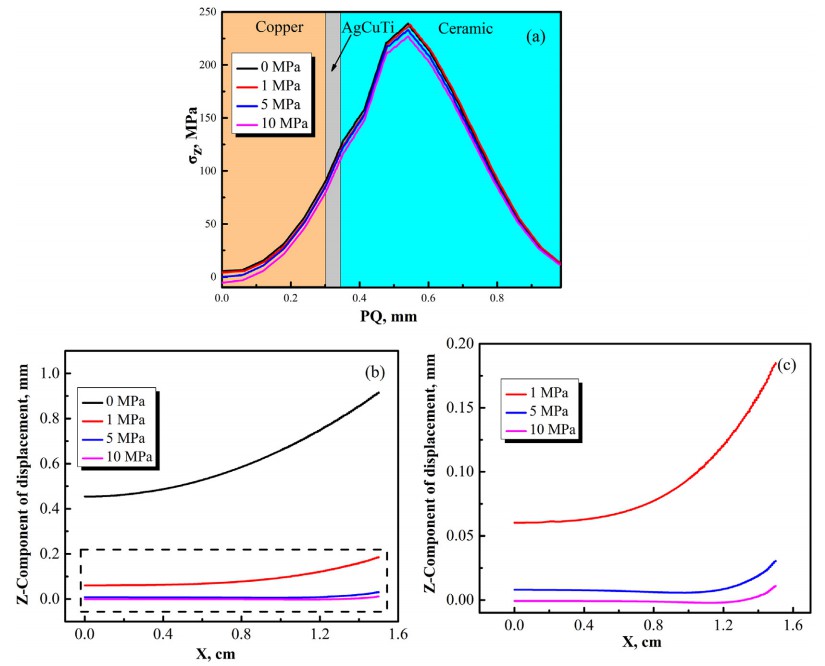
6、壓力對翹曲變形和殘余應力的影響

熱應力的產生是一個積累的過程，界面的軸向殘余應力和翹曲變形可通過在AMB陶瓷基板上施加一定的壓力來減少釬焊過程中，結果如圖9所示。隨著釬焊壓力，軸向殘余應力的分布趨勢為基本不變，但施加的壓力越大，釋放界面的軸向殘余應力。當壓力為1 MPa時，界面處的應力與未施加壓力時相同。然而，在 10 MPa 基底壓力下，軸向殘余應力降低到227 MPa。同時，壓力不宜過大，否則會導致陶瓷破裂和焊料溢出。圖10(a)顯示了沿 PQ 路徑的 σz 分布，適用于不同的壓力基板。圖10（b）顯示了Z分量沿MN路徑和圖10（c）顯示了放大的區域。